시간복잡도를 통한 수행시간 예측하기
자료의 크기와 시간복잡도를 이용하여 수행시간 예측하기 - O(N^3), O(N^2), O(NlogN), O(N)
- 최 대 연속 부분 구간 합 문제
1차원 배열에서 연속된 부분 구간 중 그 합이 최대인 구간을 찾는 문제
ex) 배열 [-7, 4, -3, 6, 3, -8, 3, 4]에서 최대 합을 갖는 부분 구간은 [4, -3, 6, 3]으로 그 합은 10 - O(N^3) 알고리즘
const int MIN = numeric_limits<int>::min(); // A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(N^3) int inefficientMaxSum(const vector<int>& A) { int N = A.size(), ret = MIN; for(int i = 0; i < N; ++i) for(int j = i; j < N; ++j) { // 구간 A[i..j]의 합을 구한다. int sum = 0; for(int k = i; k <= j; ++k) sum += A[k]; ret = max(ret, sum); } return ret; } - O(N^2) 알고리즘
const int MIN = numeric_limits<int>::min(); // A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(N^2) int betterMaxSum(const vector<int>& A) { int N = A.size(), ret = MIN; for(int i = 0; i < N; ++i) { int sum = 0; for(int j = i; j < N; ++j) { // 구간 A[i..j]의 합을 구한다. sum += A[j]; ret = max(ret, sum); } } return ret; } - O(NlogN) 알고리즘
// A[lo..hi]의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(NlogN) int fastMaxSum(const vector<int>& A, int lo, int hi) { // 기저 사례: 구간의 길이가 1일 경우 if(lo == hi) return A[lo]; // 배열을 A[lo..mid], A[mid+1..hi]의 두 조각으로 나눈다. int mid = (lo + hi) / 2; // 두 부분에 모두 걸쳐 있는 최대 합 구간을 찾는다. 이 구간은 // A[i..mid]와 A[mid+1..j] 형태를 갖는 구간의 합으로 이루어진다. // A[i..mid] 형태를 갖는 최대 구간을 찾는다. int left = MIN, right = MIN, sum = 0; for(int i = mid; i >= lo; --i) { sum += A[i]; left = max(left, sum); } // A[mid+1..j] 형태를 갖는 최대 구간을 찾는다. sum = 0; for(int j = mid+1; j <= hi; ++j) { sum += A[j]; right = max(right, sum); } // 최대 구간이 두 조각 중 하나에만 속해 있는 경우의 답을 재귀 호출로 찾는다. int single = max(fastMaxSum(A, lo, mid),fastMaxSum(A, mid+1, hi)); // 두 경우 중 최대치를 반환한다. return max(left + right, single); } - O(NlogN) 알고리즘
// A[] 의 연속된 부분 구간의 최대 합을 구한다. 시간 복잡도: O(n) int fastestMaxSum(const vector<int>& A) { int N = A.size(), ret = MIN, psum = 0; for(int i = 0; i < N; ++i) { psum = max(psum, 0) + A[i]; ret = max(psum, ret); } return ret; }
시간복잡도 별 알고리즘의 속도 비교
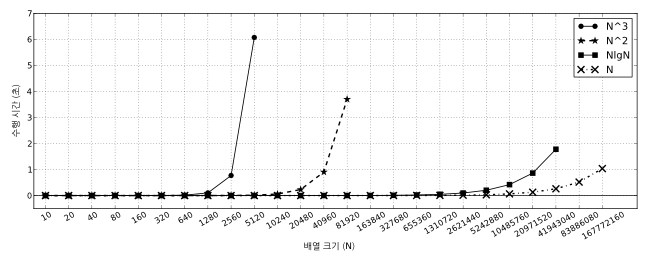
정리
- O(N^3) : 크기 2560인 입력까지를 1초 안에 풀 수 있음 (2560^3은 대략 160억)
- O(N^2) : 크기 40960인 입력까지를 1초 안에 풀 수 있음 (40960^2은 대략 16억)
- O(NlogN) : 크기가 대략 2천만인 입력까지를 1초 안에 풀 수 있음 (NlogN은 대략 5억)
-
O(N) 알고리즘 : 크기가 대략 1억 6천만인 입력까지를 1초 안에 풀 수 있음
- 인프라 사양에 따라 결과는 달라질수 있음 위에 수치들은 어디까지나 예측값
참고 사이트
book.algospot : https://book.algospot.com/estimation.html