특징

  • 추세나 계절성이 있는 시계열은 서로 다른 시간에 시계열의 값에 영향을 줄 것이기 때문에 정상성을 나타내는 시계열이 아님
  • 백색잡음(white noise) 시계열 : 정상성을 나타내는 시계열 (언제 관찰하는지 상관이 없고 시간에 따라 어떤 시점에서 보더라도 똑같이 보일 것이기 때문.)

  • 주기성 행동을 가지고 있지만 추세나 계절성은 없는 시계열 : 정상성을 나타내는 시계열 (주기가 고정된 길이를 갖고 있지 않기 때문, 시계열을 관측하기 전에 주기의 고점이나 저점이 어디일지 확실하게 알 수 없음)

  • 일반적으로는, 정상성을 나타내는 시계열은 어떤 주기적인 행동이 있을 수 있더라도 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않음
  • 시간 그래프는 시계열이 일정한 분산을 갖고 대략적으로 평평하게 보임

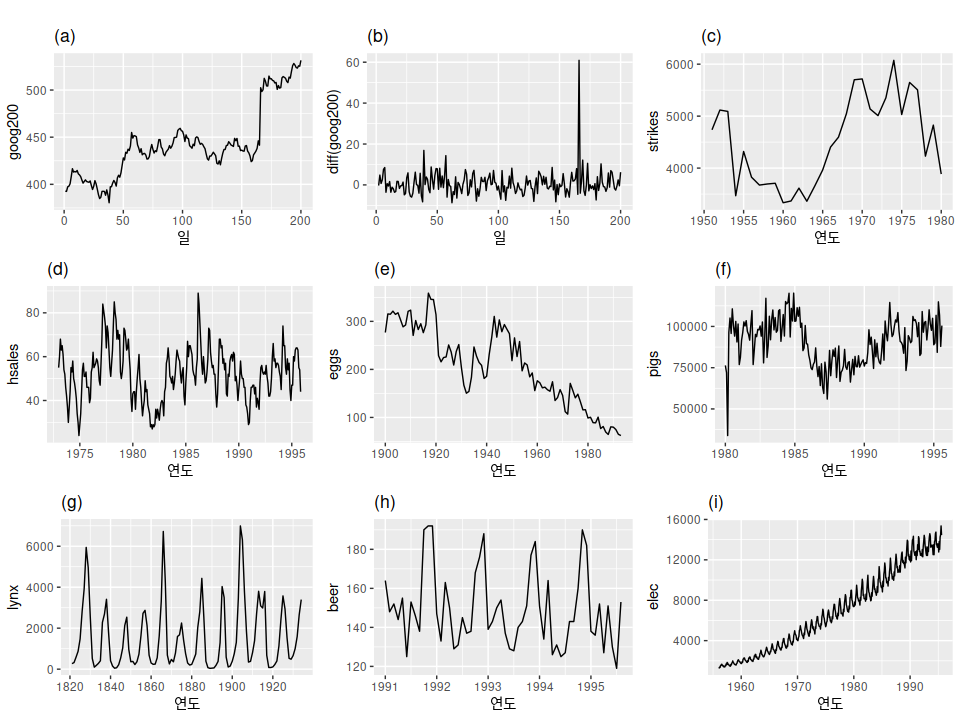
select

Figure 8.1: (a) 200 거래일 동안의 구글 주식 가격 (b) 200 거래일 동안의 구글 주식 가격의 일일 변동 (c) 미국의 연간 파업 수 (d) 미국에서 판매되는 새로운 단독 주택의 월별 판매액 (e) 미국에서 계란 12개의 연간 가격 (고정 달러) (f) 호주 빅토리아 주에서 매월 도살한 돼지의 전체 수 (g) 캐나다 북서부의 맥킨지 강 지역에서 연간 포획된 스라소니의 전체 수 (h) 호주 월별 맥주 생산량; (i) 호주 월별 전기 생산량.

Q. 위 그림 중 정상성을 나타내는 시계열은?

  1. 분명하게 계절성이 보이는 (d), (h), (i)는 후보가 되지 못함
  2. 추세가 있고 수준이 변하는 (a), (c), (e), (f), (i)도 후보가 되지 못함
  3. 분산이 증가하는 (i)도 후보가 되지 못함

A. (g)

  • 언뜻 보면 시계열 (g)에서 나타나는 뚜렷한 주기(cycle) 때문에 정상성을 나타내는 시계열이 아닌 것처럼 보일 수 있음.
  • 하지만 이러한 주기는 불규칙적(aperiodic)임. 먹이를 구하기 힘들만큼 살쾡이 개체수가 너무 많이 늘어나 번식을 멈춰서, 개체수가 작은 숫자로 줄어들고, 그 다음 먹이를 구할 수 있게 되어 개체수가 다시 늘어나는 식이기 때문.
  • 장기적으로 볼 때, 이러한 주기의 시작이나 끝은 예측할 수 없음. 따라서 이 시계열은 정상성을 나타내는 시계열.

참고 사이트

  • otexts : https://otexts.com/fppkr/stationarity.html#fig:stationary